Research
Deep learning for gauge theories
Lattice gauge theories play a pivotal role in our understanding of fundamental physics in nature, particularly in the realm of quantum chromodynamics (QCD), which governs the strong nuclear force. QCD, a non-abelian gauge theory, describes the interactions between quarks and gluons, the elementary constituents of protons and neutrons. Despite its simple formulation, the non-perturbative regime of QCD exhibits remarkably complex phenomena, including confinement and chiral symmetry breaking. Monte Carlo methods have led to profound insights into the behaviour of these theories at strong coupling, and produced remarkable results such as computation of hadron masses from first principles. Despite the tremendous progress made over the last four decades, fundamental stumbling blocks such as the sign problem and the inability to simulate real-time dynamics still remain.
We are actively investigating the use of neural networks to model the ground-state wavefunctions of lattice gauge theories. Our previous work has included studying discrete gauge theories using gauge-equivariant convolutional neural networks. We identified the distinct topological phases and the confinement phase transition in these systems. For Z2 theories, we probed the continuous transition and computed critical exponents, with excellent agreement with previous Monte Carlo simulations and the conformal bootstrap. These findings suggest that so-called neural-network quantum states are a promising method for precision studies of lattice gauge theory.
Numerical and machine-learning methods for string theory
Numerical methods have become increasingly important in string theory, particularly for understanding the geometry of Calabi-Yau manifolds. These mathematical objects are essential for constructing realistic particle physics models from string theory, but their complexity all but precludes analytical solutions. Our work has focused on developing and applying novel computational techniques to address these challenges.
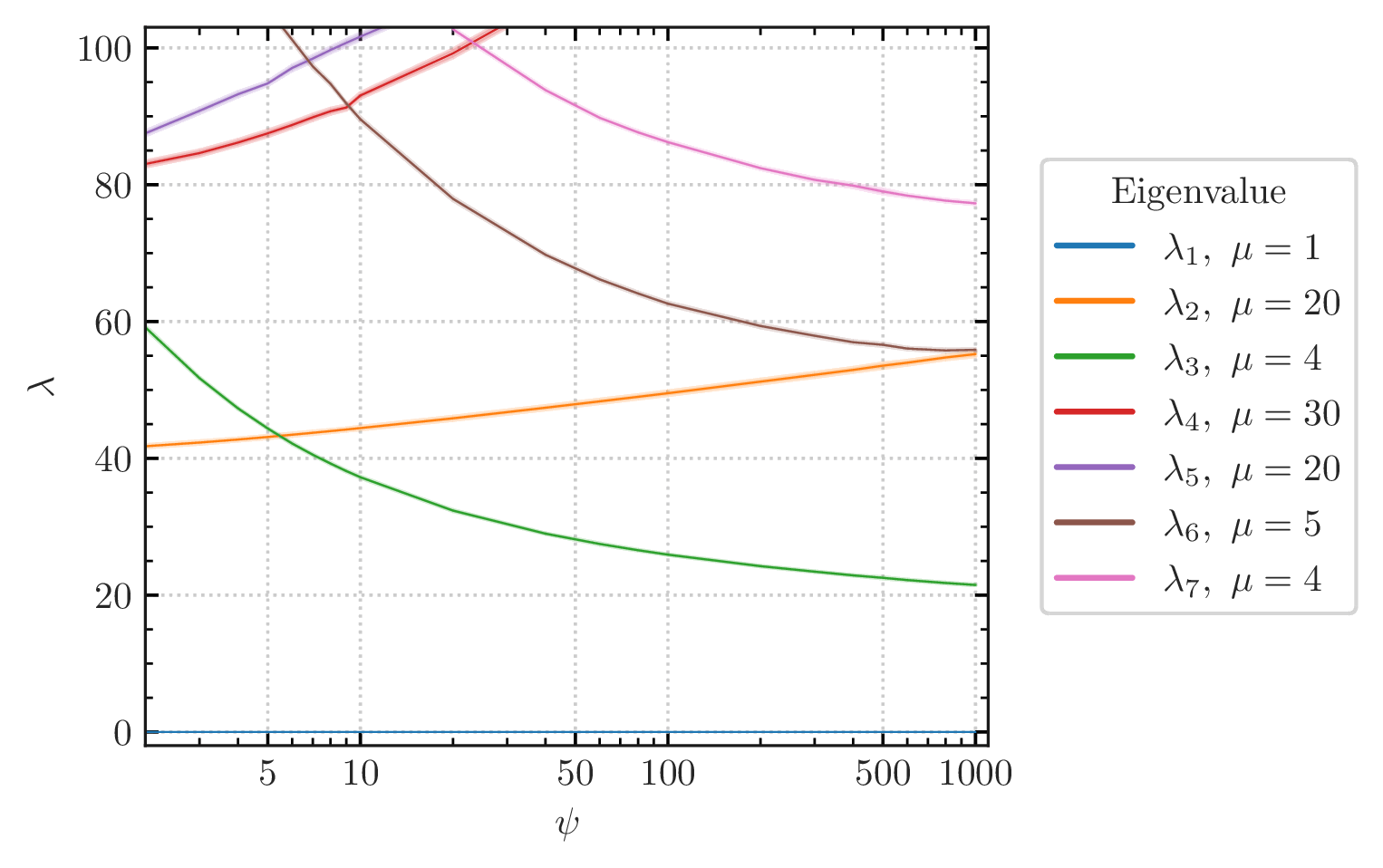
One of our contributions has been the application of machine-learning techniques to compute Calabi-Yau metrics and hermitian Yang-Mills connections. We have demonstrated that neural networks can be trained to approximate these geometric objects with high accuracy while offering advantages in speed and scalability compared to traditional numerical methods. Our work on line bundles over elliptic curves, K3 surfaces, and quintic threefolds shows promise for extending these techniques to more complex scenarios relevant to particle physics model building.
Another important aspect of our research has been the numerical investigation of the Swampland Distance Conjecture. By computing moduli-dependent Kaluza-Klein towers on Calabi-Yau manifolds, we have provided concrete evidence for the conjecture’s predictions about the behavior of effective field theories at large distances in field space. Our work on the one-parameter family of quintic Calabi-Yau manifolds has yielded insights into the rate at which states become exponentially light, confirming the conjecture’s expectations.
These numerical approaches open up new avenues for exploring string theory phenomenology. By enabling more accurate calculations of metrics, connections, and spectra, they pave the way for computing physical quantities such as Yukawa couplings in string compactifications. However, challenges remain, including extending these methods to higher-dimensional moduli spaces and non-abelian gauge bundles. As these techniques continue to evolve, they promise to play an increasingly important role in connecting string theory to observable physics and in exploring the vast landscape of string vacua.
Geometric structures in supergravity and string theory
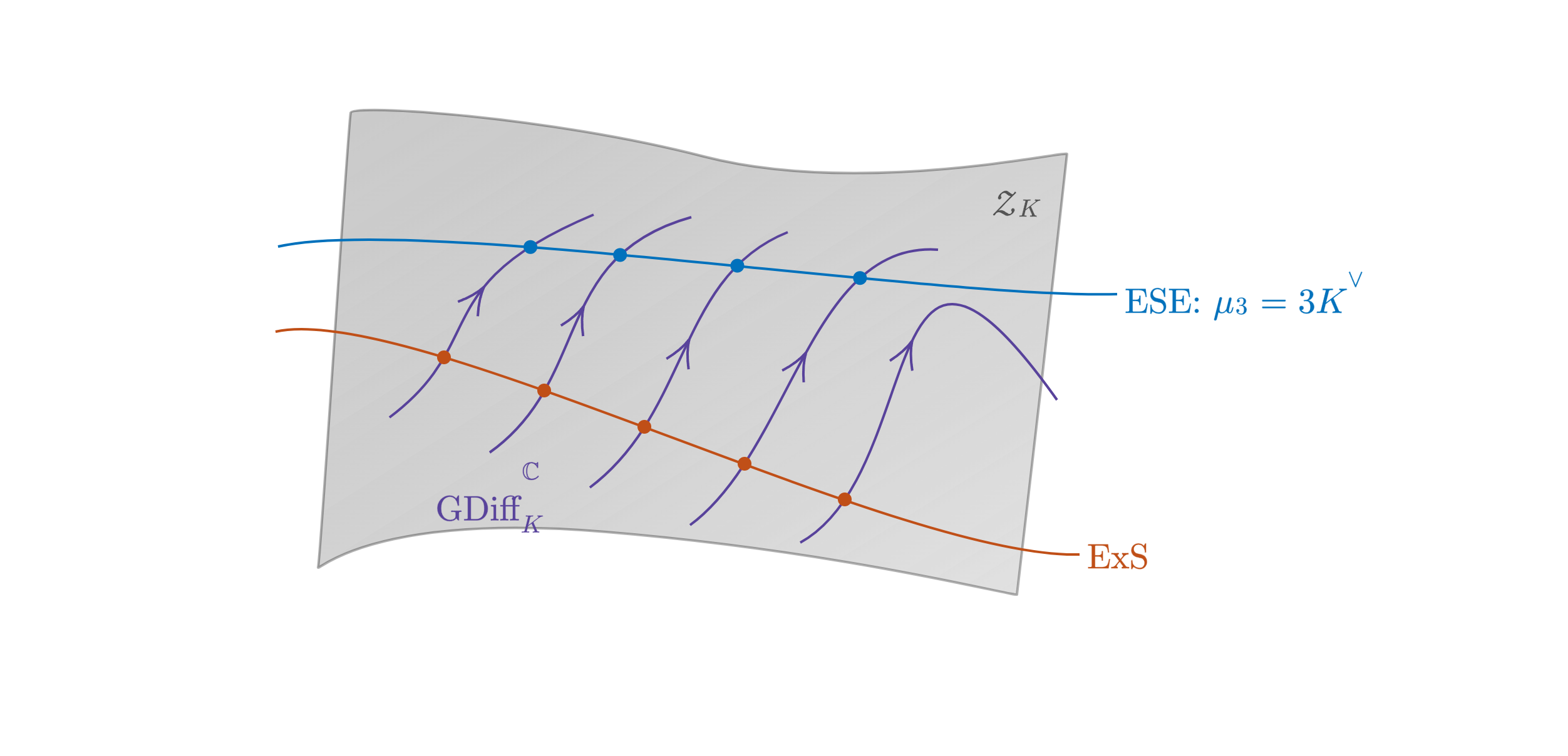
Our work on geometric structures focuses on those that appear in supergravity and string theory, with a particular emphasis on supersymmetric solutions. We have developed systematic approaches to classify and analyse these solutions using $G$-structures and generalised geometry. We have also studied the relationship between supersymmetry and geometric flows in heterotic supergravity. In particular, we showed how anomaly flow can be derived from a functional related to the bosonic string action, providing new tools for constructing solutions. Open problems we are interested in include finding a geometric dual to $c$-extremization for general flux backgrounds in M-theory and understanding the landscape of AdS3 vacua with small cosmological constants.
String model building and phenomenology
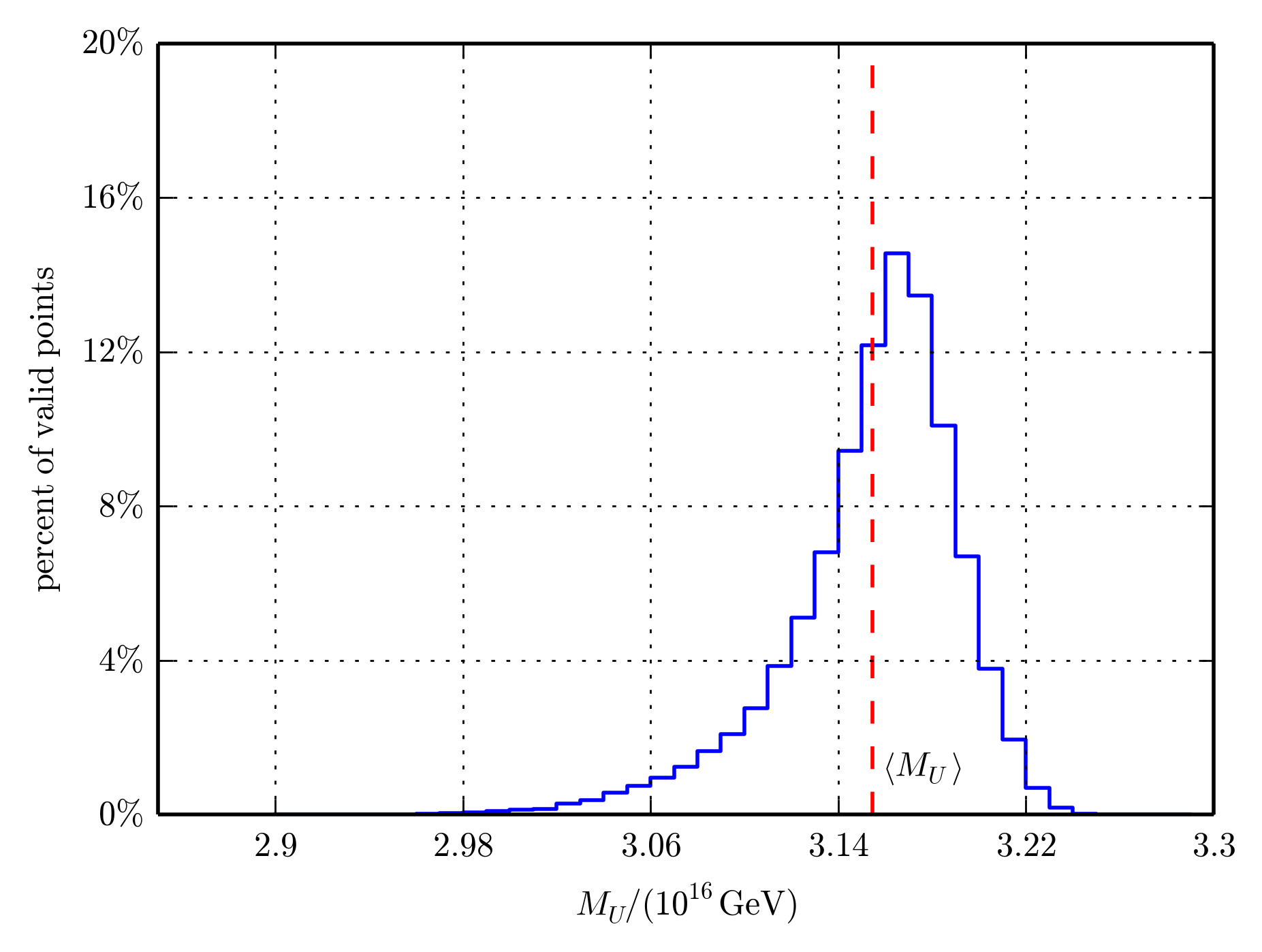
String theory provides a promising framework for unifying gravity with the other fundamental forces of nature. However, connecting string theory to observable particle physics remains a significant challenge. This research thread focuses on constructing realistic string models that could describe our universe, with a particular emphasis on heterotic string theory. Our work has developed techniques for constructing vector bundles on Calabi-Yau manifolds and studying the phenomenology of specific heterotic standard models, including details of gauge coupling unification, supersymmetry breaking, and particle spectra.
Open problems in this field that we are thinking about include fully stabilizing all moduli in a controlled manner, understanding the landscape of string vacua, and making concrete predictions that can be tested experimentally.